Artificial Neural Networks
Artificial neural networks have been studied for many decades and now represent a large field within artificial intelligence. They have found applications in image processing, image reconstruction, image recognition, extrapolating data, symbolic regression, classification, control, video games and even art.
Biological Neuron
As artificial neural networks take their inspiration from their biological counterpart it seems fitting to introduce these first. Neurons are used by nearly all animals (excluding sponges and trichoplaxs) to process internal and external stimuli in order to determine their actions. For many animals there is a highly complex mapping between their sensory inputs and their actions, humans being a good example, and neurons are at the heart of this complexity.
A biological neuron is depicted below with the dendrites and axon terminals shown. Neurons receive electrical signals from other neurons (or sensory inputs) via their dendrites and, depending upon the strength and timings of these inputs, transmit their own signal along their axon and out to other neurons.
Each neuron receives inputs from many neurons and their outputs go on to feed into many other neurons. This many input many output mapping means that groups of neurons become highly connected. It is this high connectivity which gives rise to the complexity which can be achieved by large groups of neurons. The strength of each of these connections can also be increased or decreased, changing how much one neuron affects another. This ability to change each connections strength (among other things) is how biological brains adapt and learn during their lifetime. A simple way in which the weight can be changed in order to learn from experiences is to strengthen the connections between neurons which lead to positive outcomes. This idea was first proposed by Donald Hebb (1949) and is therefore called the hebbian learning rule.
Biological Brain Vs. Modern Computers
It is worth making a comparison between natures evolutionary solution to computation and modern day computers in order to show why reseachers are intersted in learning from biology. For this comparison we shall be using the human brain and Intel's Quad-Core + GPU Core i7 processor released in 2012.
The average human brain is through to contain around 100 billion neurons each with approximately 7000 connections; hence the high connectivity (700 trillion!). Each neuron can be as small as 0.004 mm in size. When neurons die the global operation of the animal is unaffected; that is to say neural networks are very fault tolerant. The average power consumption of a human brain is thought to be around 20W.
The Core i7 contains 1.4 billion transistors each with two inputs and one output. Each transistor in this processor is 0.00000022 mm in size. If a single transistor were to fail in the CPU (central processing unit) of a Core i7 the whole computer would fail to function; not at all fault tolerant. The power consumption of this Core i7 when under load is approximately 200W.
Furthermore there is no central control system in the human brain and each neuron operates independently and in parallel. In contrast modern computers are controlled by their CPU and operate sequentially. It is also interesting how the two methods store information. Modern computers have dedicated memory banks into which data is save and retrieved when needed. Neural networks however store information in their very configuration by adjusting the arrangement of neurons and their connection strengths, there is no "hard drive", processing and information storage is done together.
It is clear that human brains are far more powerful than computers; we are creative, adaptive and possess consciousness. It is also clear that the neurons highly connected architecture has many advantages including fault tolerance, power consumption, parallel processing and integrated data storage. For these reasons, and others, the study of neurons as computational devises has been ongoing since the 1940's; starting with the neurophysiologist Warren McCulloch and a mathematician Walter Pitts.
The Artificial Neuron
The idea behind an artificial neuron is to model the behaviour of real neurons as simply as possible without losing aspects which make them so powerful. The reason for making simple models is to make the neurons easier to study and to make simulating them computationally viable; the more complex the models are the longer any simulation would take to complete. Nearly all artificial neurons can be described by the diagram below; with the activation function changing from model to model. Here each neuron input is multiplied by a weight associated with the connection and then each weighted input is summed before being passed into an activation function.
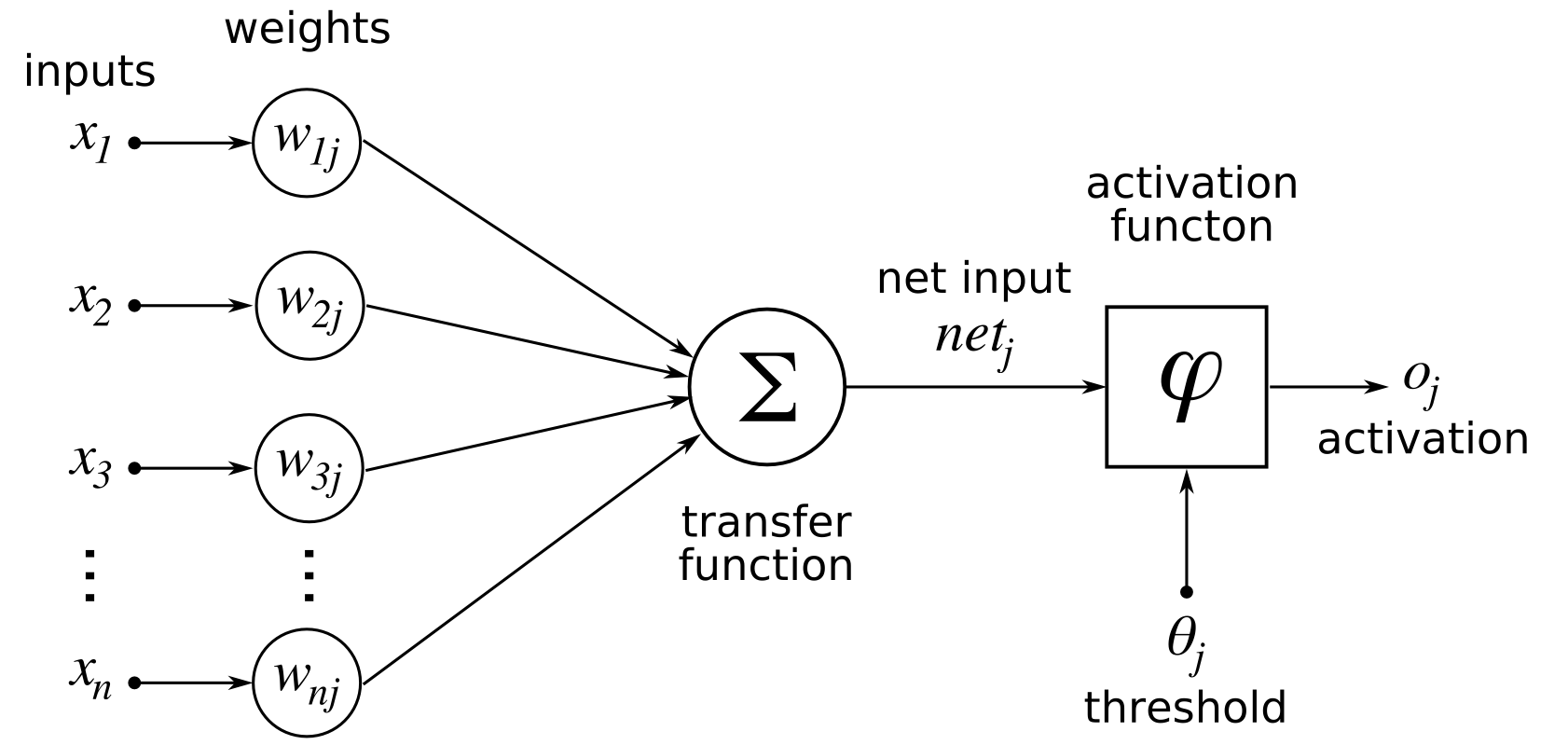
As mentioned the first artificial neural network was developed by Warren McCulloch and Walter Pitts in what is referred to as the McCulloch–Pitts model. This model is very simple, the output of each neuron is set as one if the sum of the weighted inputs is greater than a internal threshold or set to zero otherwise.
Although much has changed since the 1940's this basic model is still representative of many models today. Major developments to the neuron models include changes to the mapping between inputs and output to be more complex and adding dependencies on the timings of the inputs.
Training Artificial Neural Networks
In order to use an artificial neural network they first need to be configured towards a certain task. This process of configuring an artificial neural network is refereed to as training or learning; taking the terminology from biology where animals learn from their environments. There are many training methods for artificial neural network found in the literature and each have their own advantages and disadvantages towards certain tasks. The most famous training methods include Back Propagation, Restricted Boltzmann Machines, Hopfield Networks and Radial Basis Function Networks.
